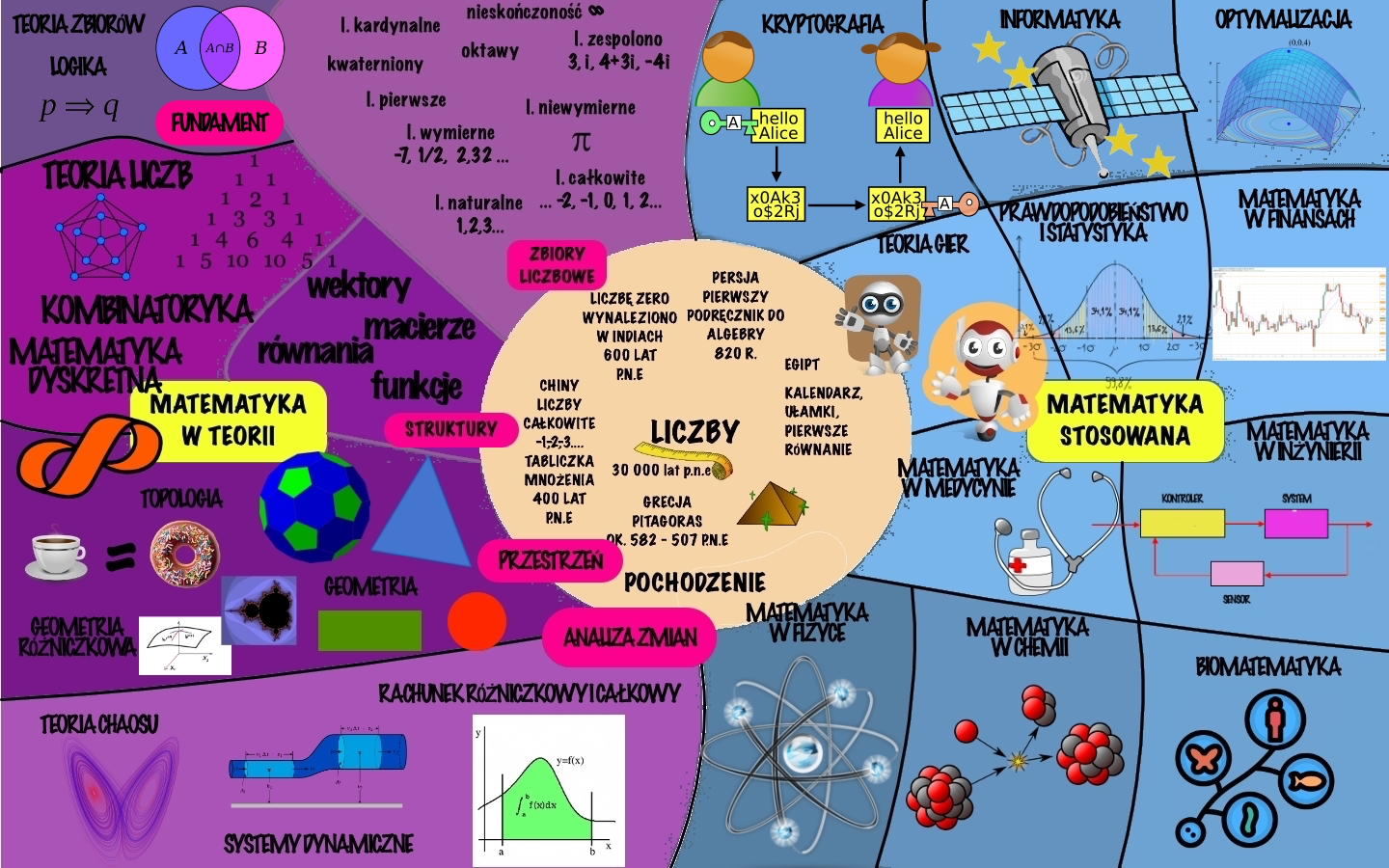
Matematyka, z którą spotykamy się w szkole nie obejmuje wszystkich dziedzin tego przedmiotu. Poznajemy tylko fragment tej wspaniałej i bardzo różnorodnej dziedziny nauki. Moim celem jest pokazanie wieloaspektowości i uniwersalności Królowej Nauk.
Początki matematyki związane są z początkiem ludzkości. Pierwsze dowody na to, że ludzie potrafili liczyć sięgają już 30 000 p.n.e. Z tego okresu znaleziono kości zawierające ślady nacięć, które uważane są za próbę liczenia.
Egipcjanie opracowali kalendarz, posługiwali się ułamkami i rozwiązywali podstawowe równania. Twierdzenie Pitagorasa jest najbardziej rozpowszechnionym dowodem matematycznym w starożytności. Liczby całkowite pojawiły się w Chinach, a zero po raz pierwszy użyto w Indiach. Algebra jest jednym z najstarszych działów matematyki. Najstarszy tekst matematyczny pochodzi z Persji.
Teraz dokonam wielkiego skok w czasie. Przejdę do matematyki związanej z czasami nowożytnymi. Nowoczesna matematyka może być zasadniczo podzielona na matematykę teoretyczną i matematykę stosowaną.
Matematyka teoretyczna i matematyka stosowana bardzo się z sobą łączą.
Przyjrzyjmy się pewnej sytuacji. Osoba, która lubi zajmować się liczeniem z czystej ciekawości siada przy biurku i rozwiązuje abstrakcyjne problemy. W tym momencie wpada na nowe rozwiązania, postawionych wcześniej problemów, które jednak nie mają zastosowania w praktyce. Jakiś czas później naukowiec zajmujący się np. rozwiązaniem problemu z granicy matematyki i fizyki lub informatyki odkrywa, że właśnie to równanie sprzed 100 lat jest idealnym rozwiązaniem, które praktycznie przekłada się na unowocześnienie technologii czy też nowe odkrycie w nauce.
Jeżeli chodzi o dziedziny matematyki teoretycznej możemy je uporządkować według kategorii.
Zbiory liczbowe – jako pierwsze poznajemy liczby naturalne, na których wykonujemy podstawowe działania. Kolejne zbiory liczbowe to: zbiór liczb całkowitych, wymiernych, niewymiernych i liczby zespolone. Wprowadzono też kwaterniony i oktawy, które wykorzystywane są w programowaniu. Liczby kardynalne to liczby porządkowe.
Matematyka wprowadza pewne struktury, które służą do opisywania świata zewnętrznego. Posługujemy się funkcjami, równaniami, macierzami i wektorami. Teoria liczb bada właściwość liczb pierwszych, kombinatoryka zajmuje się badaniem właściwości niektórych struktur takich jak drzewa i grafy. Matematyka dyskretna, popularna w informatyce, zajmuje się strukturami skończonymi. Skończona jest liczba liczb, skończona jest liczba operacji w jednostkach czasu pracy komputera.
Geometria to dziedzina matematyki, która zajmuje się badaniem kształtów i tym jak one zachowują się w przestrzeni. Początki geometrii związane są z bryłami platońskimi i twierdzeniem Pitagorasa. Geometria jest bliska trygonometrii. Jestem pewien, że wszyscy znają ją ze szkoły. Nowością jest geometria fraktalna, która zajmuje się obiektami samopodobnymi. Oznacza to, że dowolny fragment zbioru odpowiednio powiększony, przypomina do złudzenia cały zbiór lub jego znaczną część.
Topologia jest nauką badającą te właściwości geometryczne, które nie zmieniają się przy przekształceniach takich jak: rozciąganie, skręcanie albo obroty np. kubek może być przekształcony na pączek.
Geometria różniczkowa bada krzywe, powierzchnie i ich wielowymiarowe uogólnienia.
Przejdźmy do następnej kategorii, która opisuje zmiany. Rachunek różniczkowy i całkowy jest jednym z największych osiągnięć matematyki. Różniczkowanie odnosi się przede wszystkim do zagadnień związanych z prędkością, przyspieszeniem, nachyleniem i krzywizną krzywych. Całkowanie wiąże się z obliczaniem pól powierzchni, objętości i pojęciem środka ciężkości. Wiedza ta jest częścią analizy matematycznej.
Tutaj również znajdziemy systemy dynamiczne i teorię chaosu. Systemy dynamiczne opisują zamianę stanu materii lub zachowanie elementów w ekosystemach. Teoria chaosu szczegółowo bada początki zachodzących procesów np. w przyrodzie lub w ekonomii.
Przedstawiony podział matematyki teoretycznej powinien wyglądać jak sieć łącząca ze sobą wiele elementów z różnych dziedzin. Stopień powiązania jest tak duży, że nie można uprawiać tych dziedzin oddzielnie.
Wreszcie przechodzimy do matematyki stosowanej. Bez matematyki nie istnieje fizyka. Matematyka jest również używana w innych dziedzinach nauki takich jak chemia i biomatematyka. Te dwie dziedziny zajmują się badaniem np. atomów i ewolucją gatunków.
Matematyka w medycynie pomaga wykrywać i namierzać nowotwory. Laboratoria korzystają z modeli matematycznych, aby skrócić pracę nad tworzeniem leków. Codzienna dawka leków to też matematyka.
Matematykę również używamy w inżynierii. Już od czasów Egipcjan w projektowaniu budynków używa się matematycznych wzorów. Bardzo skomplikowane układy elektryczne wykorzystywane w samolotach czy elektrowniach używają matematycznych systemów do kontroli zachodzących w nich procesów.
Teoria gier pomaga grającym osobom, które podejmują ważne decyzje w wybraniu najlepszej opcji, ma też swoje zastosowanie w ekonomii, socjologii i psychologii.
Prawdopodobieństwo bada przypadkowość zachodzących zjawisk takich jak np. rzut monetą lub gra w kości. BARDZO TO W TYM MOMENCIE UPROŚCIŁEM Prawdopodobieństwo bardzo często wykorzystywane jest np. w przemyśle. Statystyka jest nauką badającą losowość. Przy zbieraniu dużej liczby danych ma zastosowanie w matematyce finansowej, która między innymi pokazuje trendy giełdowe i walutowe. Ściśle z tym związana jest optymalizacja, która wybiera najlepsze rozwiązania wśród istniejących opcji. Optymalizacja ma zastosowanie w rzeczach bardzo konkretnych i abstrakcyjnych, począwszy od lokowania pieniędzy a skończywszy na sposobach osiągnięcia szczęścia.
Informatyka ściśle związana z systemem jedynkowym. Aktualnie pracuje się nad zbudowaniem sztucznej inteligencji i tutaj mają zastosowania różne dziedziny matematyki teoretycznej.
Teoria kryptografii jest bardzo ważna dla informatyki i zabezpiecza połączenia internetowe między nami. Nikt nie mógłby robić zakupów, opłacać rachunków i czuć się bezpiecznie w internecie bez matematyki. Kryptografia wykorzystuje dużo teoretycznej matematyki kombinatorykę i teorię liczb.
Fundamentem matematyki jest teoria zbiorów i logika. Teoria zbiorów na początku wzbudzała wiele kontrowersji, jednak wraz z rozwojem matematyki zaczęła pełnić rolę fundamentu, na którym opiera się większość matematycznych rozważań.
Rozwój logiki jest połączony z pojawieniem się abstrakcyjnych form rozumowania. Historycznie związany jest z rozkwitem filozofii, obecnie wiąże się z rozwojem matematyki.
To co przedstawiłem, definiuje matematykę teoretyczną i stosowaną.
Czy matematyka jest układem zamkniętym? Wszystkie jej elementy są ze sobą spójne. Powstaje pytanie czy matematyka to skończony zestaw aksjomatów i czy wreszcie możemy udowodnić, że ten układ jest zamknięty?
Stwarza to podejrzenie, że to wszystko jest wymyślone przez człowieka. Dziwne jest, że jakiś system wymyślony przez człowieka wyjaśnia tyle rzeczy zachodzących we wszechświecie.
Z drugiej strony, nie jesteśmy jeszcze w stanie wyjaśnić wszystkich zachodzących procesów. Zatem matematyka może być jeszcze niekompletna. Nigdy nie jesteśmy w stanie odkryć jej wszystkich reguł.
Patrząc na naukę, czasami rzecz, która wydaje się skomplikowana, staje się bardzo łatwa przy użyciu matematyki i potęgi umysłu. Czuję się wspaniale, kiedy za pomocą zasad matematycznych potrafię sobie wyjaśnić cuda w otaczającym mnie świecie. To co wydaje się skomplikowane, jest naprawdę proste i matematyka w tym wszystkim pomaga.
Będę cieszył się, jeśli zainteresujecie się tym przedmiotem. Jeśli się podobało, pokaż znajomym.
Przygotowane na podstawie filmu: „The Map of Mathematics” Domain of Science